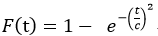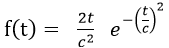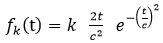マネックス証券 小田切貴秀です。(フルネーム書いてうざったいと思う人すみません。別件でちょっと実験をしてます。お許し下さい。)
さて、前回のレイリー分布導出までの説明いかがでしたでしょうか。
最近、YouTubeの”よびのり”の「今週の積分」を、高校時代を思い出しながら視聴しています。私の高校時代は”数式をいじくる”事だけで精一杯で、その式の持つ意味などを考える余裕も頭もありませんでした。しかしながら、年月が経ってくると、式の持つ意味が実は重要と改めて気付いてきました。その思いもあり、このブログを書いております。
1. ソフトウェア開発におけるレイリーモデルの"私の"イメージ的理解
前回たどり着いたレイリーモデルを再掲します。
Rayleigh累積分布関数
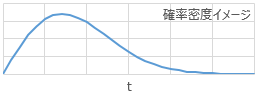
Rayleigh分布の確率密度関数
ゴンペルツ曲線、ロジステック曲線（バグ収束曲線）とちょっと違いますね。今回は違った方向からソフトウェアの不具合出現のレイリー分布のイメージを直感(こじつけ)してみたいと思います。今回は式からこじづけたあくまでも私の理解です。自分でも突っ込みどころ満載と思っています。また、ブログという限られた中で私の理解を説明するので、色々な仮定をおいて簡略化します。このような公表、議論の場がなく、文献調査も不十分です。おかしな点はご指摘いただけるとありがたいです。
1-1. ソフトウェア開発のレイリーモデルは、”因の正規分布”と”果の正規分布”の合成(と私は理解しました。）
「”因の正規分布”と”果の正規分布”の合成」と、ちょっと謎っぽく書いてみました。私のイメージする正規分布（実はもどき）は以下の２つです。不具合が発見される時期は、1)不具合の埋め込まれる(因側)の分布関数(x)と、2)埋め込まれた不具合の発覚(果側)までの分布関数(y)[要は潜伏期間]の合成から決定される時間で決まると考えました。
1-1-1 不具合の埋め込まれる(因)の分布関数f(x)
不具合の埋め込まれる分布関数ですが、プロジェクト開始時から正規分布の右半分の形をイメージしています。時間をさかのぼるのはおかしいので、t=0から出始めます。
ちなみに、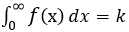
つまり、不具合の合計はk個 となるように係数を合わせています。プロジェクト開始後から始まるので、積分の下限は-∞ではなく０からです。
”標準偏差みたいなもの” と書いたのは、正規分布の半分で計算では σx はもはや標準偏差ではないためです。数式の直感的な意味は、「内在する不具合はプロジェクト開始直後が最大であり、プロジェクトが進むにつれ正規分布の形で減少していく。」ことをイメージしています。プロジェクト開始直後が一番不安定で不具合の種が存在するイメージです。時間が経つにつれ（＝プロジェクト終了近く）、不具合の種が非常に少なくなります。式の性質上、いつまでも完全には０にならないのもプロジェクトらしいと感じます。
1-1-2 埋め込まれた不具合の発覚(果)までの分布関数(y)
この分布は例えていうと、「設計書を書いたX日後に不具合を指摘された。」とか、「実装時の不具合がY日後の単体テストで見つかった。」とか、「基本設計時に存在した不具合がZヶ月後のシステムテスト時に発覚した。」とか 不具合が発覚するまでの潜伏期間のバラつきのイメージです。結合テスト時に「不具合の起因は基本設計」など、実際の不具合の分析でも良くしますね。潜伏期間の確率分布のイメージにしたものです。
ここで、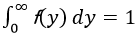
（この意味は、不具合はいつかは発覚するので確率の総和は1） 時間の開始は同じく-∞ではなく０からです。
f(x) にだけ、k がついています。
それぞれ独立なので、xとｙの確率密度関数は、単純に積で書けて、
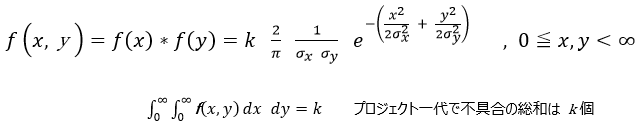
もうわからなくなってきました？？？この後は、図でイメージを表します。
1-2. 式のイメージ図とレイリー分布の導出
説明を簡単にするために、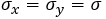
として以降を考えていきます。突っ込みどころの多いイメージです。しかし、不具合の発覚のタイミング(y)を考えると、「基本設計時の不具合が結合テスト時に出た」 とか、「実装の不具合が本番時に出た」 という状況があるので、散らばり具合のオーダーはどちらも同じくらいと考えても大差ない気がします。同じとすると、確率密度関数は、
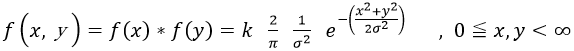
と、書き直せます。確率密度関数を３Dグラフにしてみました。
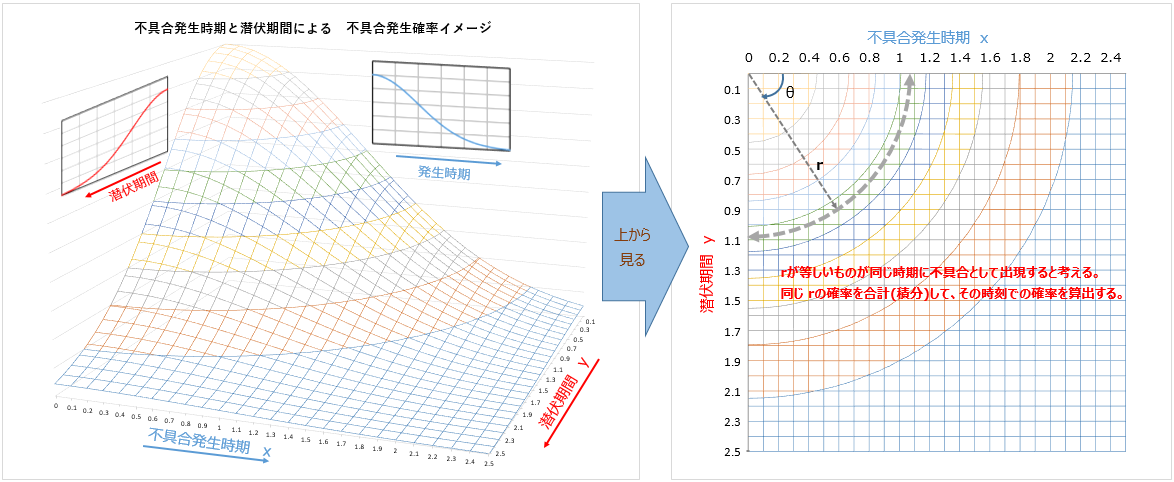
右の図で、原点から同じ距離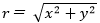 
にあるものが、同じタイミングに不具合として出ると考えます。ｒが同じになるx, yの組合せを合計（積分）するとどんな式がでるか計算してみます。 ここまでくると、極座標変換ですね。
とすると、以下の領域に変わります。
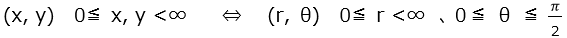
dx dy は、極座標変換 では、 r dr dθ に対応します。説明はあちこちにみられるので、紙面の関係で省略します。
確率密度関数は、同一のｒについての密度を出すので、θだけ積分します。
すると、
ここで、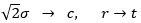
と置き換えると、
となり、見事にレイリーモデルにたどり着きました。突っ込みどころ満載過ぎて、正式な場所では相手にされないだろうことを承知の上で書いています。
ｒ(=t) の小さいところでは、確率密度が高いのですがｒ(弧の長さ)が小さいので積分の結果は小さくなり、逆にｒ(=t)の非常に大きいところは確率密度が低いので積分値が小さくなっています。従って、上述のような極大値を持つことになります。
2. レイリー分布適用した本番リリース後の不具合推定
架空のプロジェクトに対して、不具合出現のピークの位置によって、本番リリース後不具合がどのくらい出るかをシミュレーションしてみましょう。
2-1. 架空プロジェクトの前提
プロジェクトは250人月程度、期間は14ヶ月の新規開発、不具合総数は1,000件と仮定します*1。ウォータフォール開発として、それぞれの期間は下表（単位 ヶ月）とします。*2
| 要件定義 | 基本設計 | 詳細設計 | 実装 | 単体 テスト |
結合 テスト |
総合 テスト |
移行 リリース |
|---|---|---|---|---|---|---|---|
| 1ヶ月 | 2ヶ月 | 1.5ヶ月 | 2ヶ月 | 1.5ヶ月 | 3ヶ月 | 2ヶ月 | 1ヶ月 |
2-2. 不具合検出がピークになる時期のずれによる本番以降の残不具合の差
スケールパラメータcを調整して、不具合出現のピークが ①詳細設計~実装の付近の場合と②結合テスト時の場合をシミュレーションしたのが下図です。
プロジェクト運営の感覚として、①詳細設計~実装時で不具合検出がピークに達している案件は仕様がさほど揺れずに安定した案件。②結合テスト時にピークでは、仕様が撚れ過ぎて単体テストでも不具合が検出できない案件をイメージしています。
グラフの右に各フェーズで出現する不具合数（＝各期間の面積）を示しました。
①詳細設計~実装で不具合検出率がピークを迎える場合は、本番では0.4%程度の不具合を残して検出される計算となりました。合計1,000件と仮定では、それなりの軽微な不具合もカウントしている仮定です。深刻度の高い不具合はその中の3%であると想定すると、4件 × 3% = 0.12件 となり、本番での重大な不具合の存在する確率は低いと、なりました。
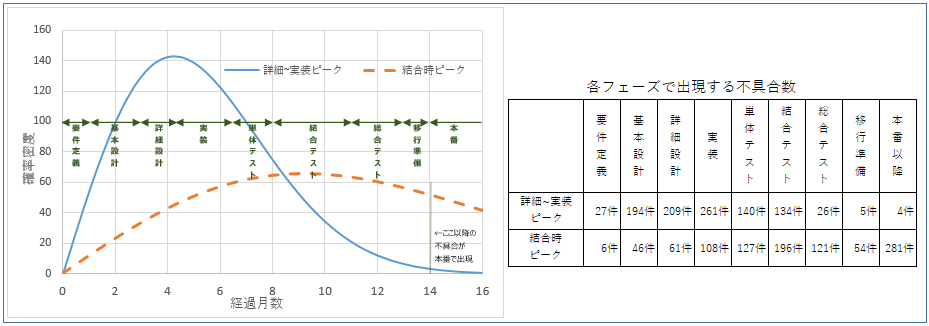
一方、②結合テスト時に確率密度が最大となる場合は、不具合を3割弱残しての本番となる計算でした。（通常はリリースを延期している案件でしょうか。）
過去のプロジェクトから見出されたモデルなので、当たり前ながら実プロジェクトとも一致する感じです。
3. 式から見る本番リリース時に不具合を減らす方法
プロジェクトを実施する場合どうしたらよいか、この数式から考えてみます。
元の式にはパラメータが３つ出てきました。k、σｘ、σｙです。この３つとも小さくすることで、本番以降に残る不具合は小さくすることができます。
| パラメータ | 意味 | 対策例 |
|---|---|---|
| k | プロジェクトに内在する 不具合総数 |
・プロジェクト開始前に決定できることはしておき、内在する不具合数を減らす。リスクを挙げ、対策をしておく。 ・プロジェクト憲章で規定できることはしておく。 ・成果物を決めておく。 ・開発手法をメンバー間で決めておく。 など |
| σｘ | プロジェクト開始時からの不具合が入る時期の広がり具合 | プロジェクトの早いフェーズで、不具合を多く出し、不具合検出のピークを迎えられるようにする。など |
| σｙ | 潜伏期間 | 成果物(状況に応じては作成中の物)などを、早期にレビューを実施することで、潜伏期間を短くする。 短時間の小まめな打合せを頻度よく行う。など |
なんだか、ソフトウェアプロジェクト管理として通常やっていることと結びつきがでました。これもあって、1-1の仮定を考えつきました。
4. おわりに
2回に渡って書きました。今回は式から内在する意味を推定してみました。今回のブログを書いていて思い出したのですが、式の持つ物理的意味を考えるようになった最初は高校で習ったニュートンの運動方程式だったと思います。
高校の教科書では、F=ma と習うのですが、それが、演習問題を解くうちに私の頭の中で、
と、再構築されたところから考えが変わりました。
数式が物理現象と結びつくんですよね。単純な算術ではなく、高等数学の式と物理現象が結びつくのが当時の私には驚きでした。そういえば、今回出てきた正規分布も考え方の一つとして、的にダーツの矢を当てようとする際、ある仮定で微分方程式を立てても、導き出されるというのも思い出しました。つまらないことをまた考えていましたね。最後はグダグダなまとめとなりましたが、またお会いしましょう。
