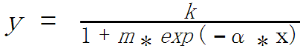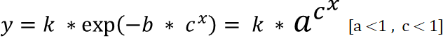こんにちは。システム開発部の小田切と申します。
前回の前編の記事いかがでしたでしょうか？
私はスマートにモデル化された微分方程式を見ると、ウキウキしてしまう性格なので、 昔を思い出して前回の記事を書いてみました。
微分方程式といわれても難しい方、
そもそも ロジステック曲線、ゴンペルツ曲線って何？という人も多く、
自分にとっては長年慣れ親しんでいた曲線や式を判りやすく書いたつもりでしたが、ご期待に沿えないところがありましたら、すみません。
とはいえ、ここまで書いてしまったので、続きを書かせて下さい。
前回の内容：
結合テストフェーズの場合、良く用いられる図に信頼度成長曲線があり、
モデルとしては、以下の２つが基本と考えられます。1)ロジスティック曲線モデル式
こちらのロジスティック曲線モデル式について成り立ちを説明致しました。2)ゴンペルツ曲線モデル式
後の説明をしやすいように前回提示の式を変形しています。
今回は、。。。
ゴンペルツ曲線について説明を致します。
こちらを使っている人の方が多いかもしれません。
ゴンペルツ曲線モデル
ロジステック関数は、1800年代に導出されたと先月説明しましたが、ゴンペルツ関数も同じく1800年代に作られました。こちらは、人の死亡率に関する関数です。
世代間で死亡率が等比級数的変化を示すとした数理モデルとして始まりました。その応用として、発見されるバグ数が等比級数的に変化するとしたモデルとして用いられています。
前回のロジスティック曲線モデルと同様に、式をイメージしやすくするために、発見バグ数をBug、時間をtとして表現してみます。
（考え方によっては、時間ｔではなくテストケース数とする場合もあるようですが、ここでは時間とします。）
こちらも考え方は単純です。
バグ発見の伸び率 d(Bug)/dt / (Bug) は、時間とともに減衰していくという考えです。
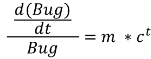[c < 1]
ちなみに、ロジスティックの場合は、
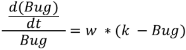でした。
ゴンペルツは、時間と共に変化率が減るという考え。
ロジスティックは、未発見バグ数が検出率に影響するという考えであることがわかります。
左辺を同じバグ発見伸び率にしたので、ゴンペルツとロジスティックの考え方の違いがお判りいただけたでしょうか。
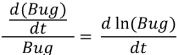と書けるので、
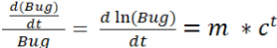となり、 t をn, n+1, n+2.... と増やすと、
毎回ｃ倍 ( 通常バグの出現率は減っていくので、c < 1 ) されていることが判ります。
上記の式から、ゴンペルツ曲線のイメージを持つには、縦軸の対数をとると判りやすいです。
ゴンペルツモデルのイメージを図にしたものが以下です。
ゴンペルツモデルの式で、tを無限大とすると、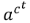
が1に近づくので、
バグの総数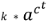
は、k に近づきます。
ロジステック曲線も、tを無限大にすると、バグ総数k が出てきましたね。全く異なる概念でできた式が似たような振舞いを示しました。
同じような曲線を描く時のパラメータの違い
最後に、実稼働90日間のテストで、1000件バグが出る場合の想定で、 ロジスティック曲線とゴンペルツ曲線の各パラメータがどのような値になるかを見てみましょう。
(注：実データではなく、パラメータの値を見るためのイメージです。)
k の値(総バグ数)以外は、お互い全く似ていないパラメータで、同じようなグラフが描けています。私は不思議さを感じます。
開発現場によってはテストの中盤以降、実際のバグ検出数を理論式にあてはめ、総バグ件数や収束時期を想定し、ソフトウェアの品質判定の目安とするところがあります。
大元の理論が判ると、実際の適用時にどうするか悩むことや、理論の限界もイメージできるのではないでしょうか。
あまりに簡単な前提で、現実は違うだろうと思う人も多いと思います。その点をイメージして頂きたく、今回２つの理論を紹介してみました。
開発フェーズ間(要件定義、基本設計…）での不具合出現件数から、本番リリース後の不具合を推定する理論があります。
これも、興味深いです。だいぶ前に実プロジェクトに適用してみたことがあります。いつかお話しできることがあると良いですね。*1
今回も長くなってしまいました。また、お会いできることを楽しみにしております。
私が昔勉強し、今回参考にした本(微分方程式を最初に見た本)は、以下です。
参考文献： ソフトウェアの品質評価法（統計的管理へのアプローチ）
三觜 武 著 日科技連出版社 1981年刊
*1: 2020/08/11 追記
ソフトウェア開発全工程での不具合数を推測する Rayleighモデル
ということで、前後編に分けて、ブログを書きました。
よろしければ、こちらもご覧ください。
https://blog.tech-monex.com/entry/2020/08/03/090729
https://blog.tech-monex.com/entry/2020/08/11/090452
